Afrique
Illustrations
1 / 5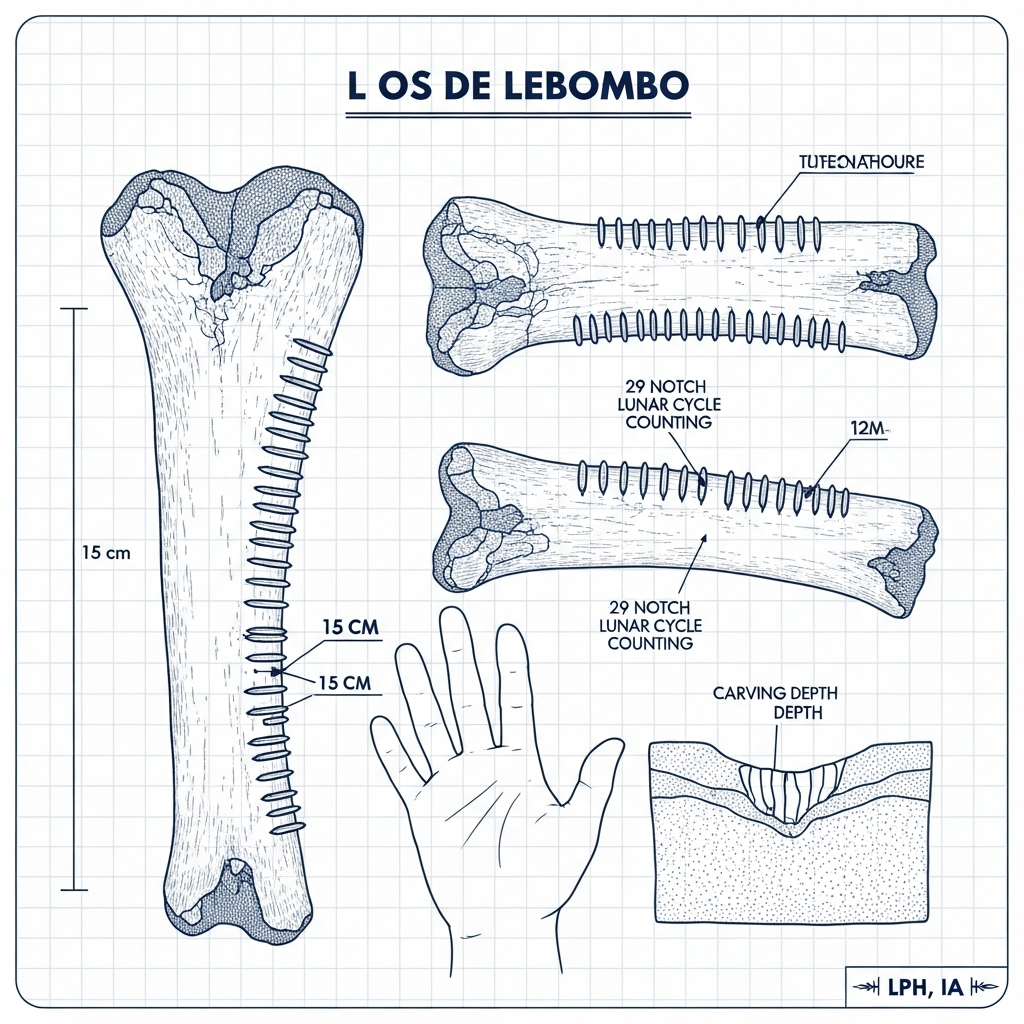
L'os de Lebombo (43 000 - 35 000 ans) : 29 encoches correspondant au cycle lunaire, découvert à Border Cave en Afrique du Sud.
Les encoches et les étoiles : Comment l'Afrique inventa les langages du calcul
Cet article couvre une période étendue, de la Préhistoire à l'Antiquité, afin de montrer la continuité des savoirs mathématiques et computationnels développés sur le continent africain.
Avant l'écriture, il y eut le comptage. Avant les temples, il y eut les cercles de pierres. Avant les ordinateurs, il y eut des systèmes binaires gravés dans la mémoire des prêtres. L'histoire que nous allons raconter ne commence pas dans les universités d'Europe ni dans les laboratoires de la Silicon Valley. Elle commence dans les grottes des montagnes Lebombo, dans les plaines du désert nubien, dans les sanctuaires des Yoruba — au cœur de l'Afrique, berceau oublié de la pensée mathématique.
Car c'est là, il y a quarante mille ans, que des mains humaines tracèrent les premières encoches délibérées sur un os de babouin. Et c'est là, des millénaires plus tard, qu'un système de divination sophistiqué utilisa le code binaire bien avant que l'Occident ne songe à l'inventer.
Hier — Les premières encoches de l'humanité
Dans les années 1970, des archéologues fouillant Border Cave, aux confins de l'Afrique du Sud et de l'Eswatini, exhumèrent un fragment de péroné de babouin. L'objet, long d'à peine quelques centimètres, portait vingt-neuf encoches distinctes, régulièrement espacées. Les datations au radiocarbone révélèrent son âge stupéfiant : entre quarante-trois mille et trente-cinq mille ans. L'os de Lebombo venait de détrôner tous les autres artefacts mathématiques connus. Il est, à ce jour, le plus ancien témoignage de pensée numérique jamais découvert.
Vingt-neuf encoches. Le nombre n'est pas anodin. Il correspond presque exactement à la durée d'un cycle lunaire. L'archéologue Claudia Zaslavsky a suggéré que la créatrice de cet outil — car il pourrait bien s'agir d'une femme — suivait peut-être les phases de la lune en relation avec son cycle menstruel. Si cette hypothèse est juste, les premières mathématiciennes de l'histoire seraient africaines, et leur arithmétique serait née d'un besoin intime de comprendre le temps qui passe.
Vingt mille ans plus tard, à l'autre bout du continent, sur les rives du lac Édouard dans l'actuelle République Démocratique du Congo, un autre os fut taillé avec une intention manifeste. L'os d'Ishango, découvert en 1950 par le géologue belge Jean de Heinzelin de Braucourt, présente des groupements d'encoches bien plus complexes que de simples marques de comptage. Les mathématiciens Dirk Huylebrouck et Vladimir Pletser y ont reconnu un système de numération en base douze, avec des sous-bases trois et quatre — une sorte de règle à calcul primitive.
Plus remarquable encore : la colonne gauche de l'os contient tous les nombres premiers entre dix et vingt. Coïncidence ? Les chercheurs en doutent. Si ces groupements sont intentionnels, alors les habitants d'Ishango, il y a vingt millénaires, auraient découvert les nombres premiers bien avant que les Grecs ne les formalisent. La pensée mathématique abstraite ne serait pas née sur les rivages de la Méditerranée, mais dans le cœur de l'Afrique équatoriale.
Ces os n'étaient pas des curiosités isolées. Ils témoignent d'une tradition de pensée systématique qui traversait le continent. Sept mille ans avant notre ère, dans le désert nubien, à cent kilomètres à l'ouest d'Abu Simbel, des peuples nomades érigèrent le plus ancien observatoire astronomique jamais construit. Nabta Playa — un cercle de pierres dressées, orienté vers le solstice d'été — précède Stonehenge de près de deux millénaires.
Les astronomes qui ont étudié le site ont identifié des alignements sur Arcturus, Sirius, Alpha Centauri, et sur la constellation d'Orion. L'astrophysicien Thomas Brophy a proposé que trois pierres intérieures représentaient les trois étoiles de la Ceinture d'Orion telles qu'elles apparaissaient dans le ciel il y a sept mille ans. Ces nomades vénérant le bétail, qui venaient de loin pour accomplir leurs rituels au moment où les pluies de mousson arrivaient, avaient développé une compréhension sophistiquée des mouvements célestes.
Des encoches sur un os aux alignements stellaires, une même impulsion traverse ces innovations : la volonté de capturer le temps, de prévoir les cycles, de transformer l'observation en connaissance reproductible. C'est le fondement même de ce que nous appelons aujourd'hui la pensée algorithmique.
Aujourd'hui — Le code binaire avant le code
Si l'os de Lebombo représente la préhistoire du calcul, le système Ifá des Yoruba en représente peut-être la première maturité. Pratiqué depuis au moins deux mille cinq cents ans dans ce qui est aujourd'hui le sud-ouest du Nigeria, ce système de divination et de connaissance utilise une structure que tout informaticien reconnaîtrait immédiatement : le code binaire.
Le système repose sur deux cent cinquante-six configurations appelées Odu, obtenues par la combinaison de seize signes principaux. Chaque Odu est représenté par huit marques organisées en quatre paires verticales. Une ligne simple signifie « ouvert » ; une ligne double signifie « fermé ». Traduit en langage moderne : un correspond à ouvert, zéro correspond à fermé. Deux puissance huit égale deux cent cinquante-six. Nous sommes face à un système de codage à huit bits, structurellement identique au code EBCDIC utilisé dans les premiers ordinateurs IBM.
Le babalawo, le prêtre d'Ifá, ne devine pas au hasard. Il calcule. À l'aide de sa chaîne divinatoire ou de seize noix de palme sacrées, il génère une séquence binaire qu'il interprète ensuite en consultant un vaste corpus de versets poétiques — des centaines de textes associés à chaque Odu, mémorisés au cours d'une formation qui commence dès l'enfance et peut durer des décennies.
L'ethnomathématicien Ron Eglash, qui a étudié les systèmes de divination par le sable au Sénégal, a reconnu dans ces pratiques un « générateur de nombres pseudo-aléatoires » et une « boucle de rétroaction numérique » — les mêmes principes que ceux qui animent les algorithmes modernes. « Voici cette boucle de rétroaction numérique absolument stupéfiante, qui est indigène », notait-il avec émerveillement.
Gottfried Wilhelm Leibniz, le philosophe et mathématicien allemand qui formalisa le système binaire en Occident au tournant du dix-huitième siècle, connaissait l'existence du système Ifá. Il l'avait découvert par l'intermédiaire de missionnaires jésuites qui avaient voyagé en Afrique et en Chine. Dans sa correspondance, Leibniz exprimait son admiration pour « la logique binaire philosophique profonde » qu'il y percevait. L'Occident redécouvrait, deux millénaires plus tard, ce que l'Afrique de l'Ouest avait codifié depuis des siècles.
Mais l'Ifá n'est pas seulement un système de calcul. C'est une base de données vivante. Chacun des deux cent cinquante-six Odu est associé à des centaines de versets — des récits mythologiques, des prescriptions rituelles, des conseils pratiques. Le corpus total dépasse probablement le million de vers. Et tout cela est conservé dans la mémoire des babalawos, transmis de génération en génération par un entraînement rigoureux qui rivalise avec les disciplines les plus exigeantes du monde académique moderne.
Les chercheurs en science et technologie africains ont souligné que ces systèmes de connaissance doivent être reconnus pour ce qu'ils sont : des technologies indigènes intelligentes. Non pas des superstitions à folkloriser, mais des innovations cognitives à étudier. L'UNESCO l'a compris, inscrivant le système Ifá au patrimoine immatériel de l'humanité en 2005.
Au-delà — Une autre voie vers l'intelligence
L'Afrique n'a pas seulement inventé le calcul binaire. Elle a aussi développé une forme de géométrie que l'Occident ne théoriserait qu'au vingtième siècle : les fractales.
En 1988, l'ingénieur américain Ron Eglash, étudiant des photographies aériennes d'un village tanzanien, fut frappé par un motif familier. Les huttes au toit de chaume étaient organisées en cercles de cercles de cercles — une structure récursive où le même schéma se répète à des échelles différentes. Eglash reconnut immédiatement ce qu'il voyait. Il avait travaillé dans la Silicon Valley. Il savait ce qu'étaient les fractales. Et il les voyait, non pas sur un écran d'ordinateur, mais dans l'architecture d'un village africain.
Ses recherches ultérieures révélèrent que cette géométrie fractale n'était pas un accident. Elle était présente dans l'urbanisme, la coiffure, les textiles, la sculpture, la peinture, le travail du métal, et jusque dans les systèmes de divination. Les artisans du Sahel fabriquaient des pare-vent en utilisant un design à échelle qui maximisait l'efficacité pour un minimum de matériau — un algorithme d'optimisation avant la lettre.
Ces découvertes obligent à repenser l'histoire des mathématiques. La récursion, l'auto-similarité, la mise à l'échelle — ces concepts que nous associons à la géométrie moderne et à l'informatique — étaient intégrés dans les pratiques quotidiennes de sociétés que l'historiographie occidentale a longtemps qualifiées de « primitives ».
Et puis il y a la mémoire. Dans les sociétés orales africaines, la connaissance n'est pas stockée dans des livres ou des disques durs. Elle est conservée dans des esprits humains, entretenus par des décennies de formation. Les « hommes de mémoire » — historiens oraux, gardiens des traditions — peuvent réciter des généalogies remontant sur des dizaines de générations, des récits historiques couvrant des siècles, des corpus poétiques de milliers de vers.
Des recherches récentes ont montré que ces systèmes de mémoire peuvent préserver des informations avec une fidélité remarquable sur des millénaires. Les traditions orales aborigènes australiennes contiennent des descriptions précises de paysages côtiers engloutis par la montée des eaux à la fin de la dernière ère glaciaire — il y a plus de sept mille ans. La mémoire humaine, correctement entraînée et socialement organisée, constitue une technologie de stockage d'une robustesse extraordinaire.
Nous vivons à une époque fascinée par les capacités de mémorisation des machines. Nos intelligences artificielles sont entraînées sur des milliards de textes, capables de régurgiter des informations avec une précision impressionnante. Mais elles restent fragiles — dépendantes de l'électricité, de la maintenance, de l'infrastructure technique. Les systèmes de mémoire africains ont survécu à des invasions, des migrations, des bouleversements politiques. Ils fonctionnent sans électricité, sans serveurs, sans mises à jour logicielles.
L'histoire de l'intelligence artificielle, telle qu'elle est habituellement racontée, commence avec Turing, avec Shannon, avec la conférence de Dartmouth en 1956. C'est une histoire de laboratoires climatisés, de circuits imprimés, de langages de programmation. Elle est vraie, mais elle est incomplète.
Car avant le silicium, il y eut l'os. Avant le code informatique, il y eut le code Ifá. Avant les algorithmes de nos machines, il y eut les algorithmes de nos ancêtres. Et beaucoup de ces ancêtres vivaient en Afrique, gravant des encoches sur des péronés de babouin, alignant des pierres sur les étoiles, transmettant de génération en génération des systèmes de calcul d'une sophistication que nous commençons à peine à reconnaître.
L'intelligence artificielle n'est pas une rupture avec le passé humain. Elle en est la continuation. Et pour comprendre où nous allons, il nous faut d'abord comprendre d'où nous venons — des grottes de Lebombo aux cercles de Nabta Playa, des sanctuaires d'Ifá aux villages fractals de Tanzanie.
Le binaire n'est pas une invention occidentale. C'est un héritage africain.